Равномерное движение
1) Средняя скорость
$$\boxed{\vec{V} = \frac {\vec S} t \text{ [м/с]}} $$
$$\vec{V} - \text{средняя скорость с учетом направления (м/с)} $$
$$\vec S - \text{перемещение с учетом направления (м)} $$
$$t - \text{время за которое сделано перемещение (с)} $$
2) Среднепутевая скорость
$$\boxed{{V} = \frac {L} t \text{ [м/с]}}$$
$$V - \text{среднепутевая скорость (м/с)}$$
$$L - \text{путь (м)}$$
$$t - \text{время (с)}$$
3) Зависимость координат от времени при равномерном прямолинейном движении
$$\boxed{X = X_{0} + V_x \cdot t \text{ [м]}}$$
$$X - \text{конечная координата тела (м)}$$
$$X_{0} - \text{начальная координата тела (м)}$$
$$V_{x} \text{ - конечная скорость тела с учетом направления (м/с)} $$
$$t \text{ - время (с) } $$
Равноускоренное движение
4) Ускорение
$$\boxed{\vec{a} = \frac {\vec Vк- \vec Vн} t \text{ [м/с²]}}$$
$$\vec{a} - \text{ускорение с учетом направления (м/с²)} $$
$$\vec Vк - \text{конечная скорость с учетом направления (м/с)} $$
$$\vec Vн - \text{начальная скорость с учетом направления (м/с)} $$
$$t -\text{ время(с)} $$
5) Зависимость координат от времени при равноускоренном движении
$$\boxed{X(t) = X_{0} + V_{0_{x}}\cdot t + {{a_{x} \cdot t^2 \over 2}} \text { [м]}}$$
$$X \text{ - конечная координата тела (м)} $$
$$X_{0} - \text{начальная координата тела (м)}\\$$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления (м/с)}$$
$$t \text{ - рассматриваемый промежуток времени (с) } $$
$$a_{x} - \text{ускорение с учетом направления (м/с²)} $$
6) Перемещение при равносукоренном движении (три формулы)
$$\boxed{ S_{x} = {V_{К_{x}}^2 - V_{0_{x}}^2 \over 2a_{x}} \text { [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{К_{x}} - \text{конечная скорость тела с учетом направления (м/с)} \\ $$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления(м/с)}\\ $$
$$a_{x} - \text{ускорение с учетом направления (м/с²)} \\ $$
$$ \boxed{S_{x} = {V_{К_{x}} + V_{0_{x}} \over 2} \cdot t \text{ [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления(м/с)} $$
$$V_{К_{x}} \text{ - конечная скорость тела с учетом направления (м/с) } $$
$$t - \text{Время} (с) $$
$$\boxed{ S_{x} = V_{0_{x}}\cdot t + {{a_{x} \cdot t^2 \over 2}} \text { [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления (м/с)}\\$$
$$a_{x} - \text{ускорение с учетом направления (м/с²)} \\$$
$$t - \text{рассматриваемый промежуток времени (с) } \\$$
7) Зависимость скорости от времени при равноускоренном движении
$$\boxed{ V_x(t) = V_{0_{x}} + {{a_{x} \cdot t}} \text { [м/c]}}\\$$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления(м/с)}$$
$$a_{x} - \text{ускорение с учетом направления (м/с²)} $$
$$t \text{ - рассматриваемый промежуток времени (с) } $$
$$V_{x} \text{ - конечная скорость тела с учетом направления (м/с)} $$
Динамика
8) Первый закон Ньютона (формулировка)
$$Первый \ закон \ Ньютона \text{ - существуют системы отсчëта, в которых тело покоится или движется равномерно прямолинейно при отсутствии действия на него сил. Такие системы называются инерциальными.} $$
9) Второй закон Ньютона
$$ \boxed{\vec{a} = \frac {\vec F} m\text{ [м/с²]}}$$
$$ \vec{a} - \text{ускорение тела с учетом направления (м/с²)} $$
$$ \vec {F} - \text{сумма всех сил действующих на тело, с учетом направления (H)} $$
$$m - \text{масса тела (кг)} $$
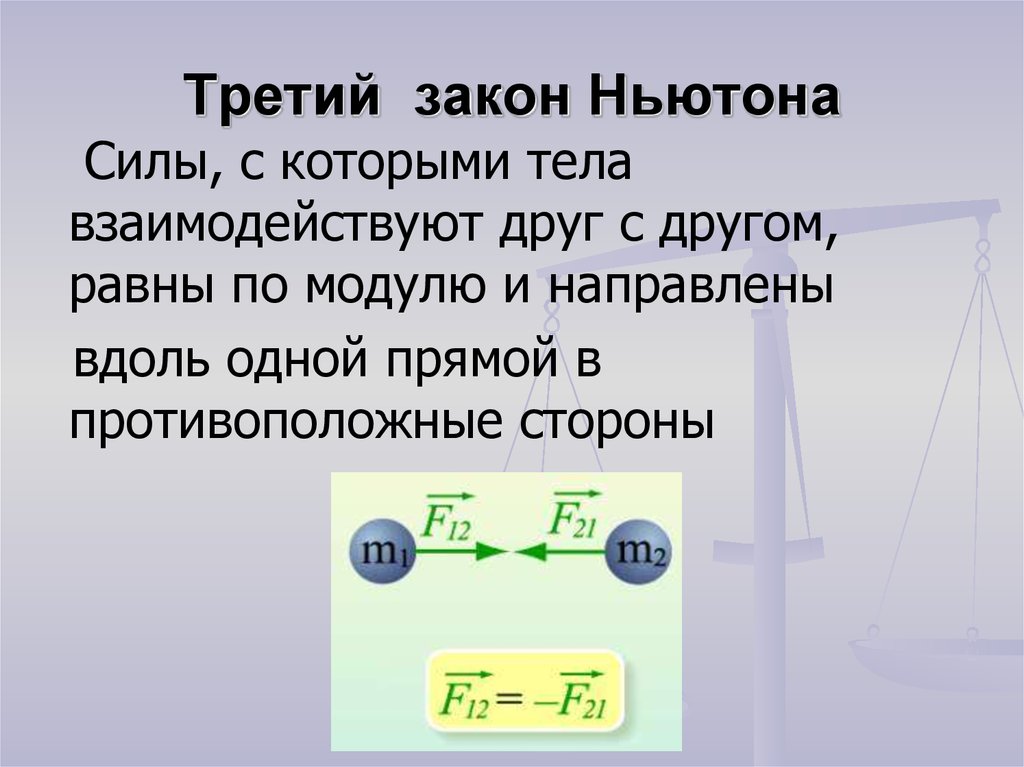
10) Третий закон Ньютона (рисунок)
$$ \boxed{\vec{F_{1_{2}}} = \vec{ -{F_{2_{1}}}}}$$
$$ \vec{F_{1_{2}}} - \text{сила, действующая на первое тело со стороны второго тела с учетом направления (H)} $$
$$ \vec{ -F_{2_{1}}} - \text{сила, действующая на второе тело со стороны первого с учетом направления (H)} $$
Третий закон Ньютона - при взаимодействии двух тел возникает пара сил, которые
1. равны по модулю
2. направлены вдоль одной прямой
3. противоположены по направлению
4. приложены к разным телам
5. силы одной природы
11) Закон гравитационного взаимодействия (без векторов)
$$ \boxed{{F} = {{G} } \cdot{m_{1} \cdot m_{2} \over r^2 } \text{ [H]}}$$
$$ {F} - \text{сила гравитационного вазимодействия (H)} $$
$$ {G} - \text{гравитационная постоянная (H · м² / кг² )} $$
$$ m_{1} , m_{2} - \text{масса взаимодействующих тел (кг)} $$
$$ r - \text{ расстояние между телами (м)} $$
12) Сила тяжести
$$ \boxed{\vec{F} = {m} \cdot {\vec{g}} \text{ [H]}}$$
$$ \vec{F} - \text{сила тяжести (H)} $$
$$ m - \text{ масса тела (кг)} $$
$$ {\vec{g}} - \text{ускорение свободного падения (м/с²)} $$
13) Сила упругости
$$ \boxed{{\vec{F}_{упр}} = {-k} \cdot {\Delta\vec{l}} \text{ [H]}}$$
$$ {\vec{F}_{упр}} - \text{сила упругости (H)} $$
$$ {k} - \text{коэффициент жесткости тела (H/м)} $$
$$ {\Delta\vec{l}} - \text{удлинение пружины (м)} $$
14) Сила трения скольжения
$$ \boxed{{{F}_{тр}} = {μ} \cdot {N} \text{ [H]}}$$
$$ {{F}_{тр}} - \text{сила трения (H)} $$
$$ {μ} - \text{коэффициент трения} $$
$$ N - \text{сила реакции опоры (H)} $$
15) Архимедова сила
$$ \boxed{{\vec{F}_{арх}} = {-ρ} \cdot {\vec{g}} \cdot {V_{погруж}}\text{ [H]}}$$
$$ {\vec{F}_{арх}} - \text{сила Архимеда (H)} $$
$$ {ρ} - \text{плотность жидкости или газа (кг/м³)} $$
$$ {\vec{g}} - \text{ускорение свободного падения (м/с²)} $$
$$ V_{погруж} - \text{ объем погруженной части тела (м³)} $$
Статика
16) Момент силы
$$ \boxed{M = {F \cdot L} \text{ [Н · м]}} $$
$$M - \text{момент силы (Н · м)}$$
$$F - \text{сила (Н)} $$
$$L - \text{плечо силы (м)} $$
17) Условия равновесия протяжённого твёрдого тела
$$\text{1) Векторная сумма всех сил, действующих на тело равно 0 . } $$
$$\text{2) Сумма всех моментов, закручивающих рычаг по часовой стрелке, равно сумме всех моментов, закручивающих рычаг против часовой стрелке.} $$
18) Коэффициент полезного действия
$$ \boxed{η = {{A_{полез} \over A_{затр}}} \ \cdot 100\% } $$
$$η - \text{К.П.Д. (%)}$$
$$A_{полез} - \text{полезная работа (Дж)}$$
$$A_{затр} - \text{вся затраченная работа (Дж)}$$
19) Давление
$$ \boxed{P = {F_{⟂} \over S} \text{ [Па]}} $$
$$ P - \text{давление (Па)}$$
$$F_{⟂} - \text{сила, действующая перпендикулярно к поверхности (Н)} $$
$$S - \text{площадь поверхности (м²)} $$
20) Плотность
$$ \boxed{{ρ} = {{m} \over {V}}\text{ [кг/м³]}}$$
$$ {ρ} - \text{плотность вещества (кг/м³)} $$
$$ m - \text{масса вещества (кг)}$$
$$ {V} - \text{ объем вещества (м³)}$$
21) Средняя плотность
$$ \boxed{{ρ} = {{m_{вся}} \over {V_{весь}}}\text{ [кг/м³]}}$$
$$ {ρ} - \text{средняя плотность (кг/м³)} $$
$${m_{вся}} - \text{вся масса тела (кг)}$$
$${V_{весь}} - \text{весь объем тела (м³)}$$
22) Гидростатическое давление
$$ \boxed{P = {ρ \cdot g \cdot h} \text{ [Па]}} $$
$$ P - \text{давление (Па)}$$
$$ρ - \text{плотность жидкости (кг/м³)} $$
$$g - \text{ускорение свободного падения (м/с²)} $$
$$h - \text{расстояние от исследуемой точки до свободной поверхности жидкости (м)} $$
23) Закон Паскаля (формулировка)
$$Закон \ Паскаля \text{ - Давление, производимое на жидкость или газ, передаëтся одинаково по всем направлениям.} $$
24) Закон гидравлического пресса
$$\boxed{{F_{1}\over {F_{2}}} = {S_{1}\over S_{2}} = {h_{2}\over h_{1}}}$$
$${F_{1}},{F_{2}} - \text{силы, действующие на поршни (Н)}$$
$${S_{1}},{S_{2}} - \text{площади поршней (м²)}$$
$$h_{1},{h_{2}} - \text{расстояния, на которые поршни смещаются (м)} $$
25) Условие плавания тел
$$ \boxed{ρ_{жидкости} \gt ρ_{тела}} $$
$$ρ_{жидкости} - \text{плотность жидкости (кг/м³)} $$
$$ρ_{тела} - \text{плотность тела (кг/м³)} $$
Законы сохранения
26) Механическая работа
$$\boxed{ {A} = {F \cdot S} \text{ [Дж]}}$$
$$A - \text{механическая работа (Дж)}$$
$$F - \text{постоянная сила, действующая на тело (Н)}$$
$$S - \text{перемещение в направлении действия силы (м)}$$
27) Мощность
$$\boxed{ {N} = {A \over t } \text{ [Вт]}}$$
$$N - \text{мощность (Вт)}$$
$$A - \text{работа (Дж)}$$
$$t - \text{время (с)}$$
28) Кинетическая энергия
$$\boxed{ {K} = {{m}\ \cdot v^2 \over 2 } \text{ [Дж]}}$$
$$K - \text{кинетическая энергия (Дж)}$$
$$m - \text{масса тела (кг)}$$
$$v - \text{скорость тела (м/с)}$$
29) Потенциальная энергия тела вблизи поверхности земли
$$\boxed{ {П} = {{m}\ \cdot g \cdot h } \text{ [Дж]}}$$
$$П - \text{потенциальная энергия (Дж)}$$
$$m - \text{масса тела (кг)}$$
$$g - \text{ускорение свободного падения (м/с²)}$$
$$h - \text{высота над поверхностью Земли (м)}$$
30) Потенциальная энергия сжатой пружины
$$\boxed{ {П} = {{k}\ \cdot \Delta x^2 \over 2 } \text{ [Дж]}}$$
$$П - \text{потенциальная энергия (Дж)}$$
$$k - \text{коэффициент жесткости пружины (Н/м)}$$
$$\Delta x - \text{величина на которую сжата или растянута пружина (м)}$$
31) Связь между работой и энергией
$$\boxed{ {Е} = {Е_{o} + А_{тр}+А_{внешн}} \text{ [Дж]}}$$
$$Е - \text{механическая энергия (Дж)}$$
$$Е_{o} - \text{начальная механическая энергия (Дж)}$$
$$А_{тр} - \text{работа внутренних сил трения (Дж)}$$
$$А_{внешн} - \text{внешняя работа (Дж)}$$
