Равномерное движение
1) Средняя скорость
$$\boxed{\vec{V} = \frac {\vec S} t \text{ [м/с]}} $$
$$\vec{V} - \text{средняя скорость с учетом направления (м/с)} $$
$$\vec S - \text{перемещение с учетом направления (м)} $$
$$t - \text{время за которое сделано перемещение (с)} $$
2) Среднепутевая скорость
$$\boxed{{V} = \frac {L} t \text{ [м/с]}}$$
$$V - \text{среднепутевая скорость (м/с)}$$
$$L - \text{путь (м)}$$
$$t - \text{время (с)}$$
Равноускоренное движение
3) Зависимость координат от времени при равноускоренном движении
$$\boxed{X(t) = X_{0} + V_{0_{x}}\cdot t + {{a_{x} \cdot t^2 \over 2}} \text { [м]}}$$
$$X_{0} - \text{начальная координата тела (м)}\\$$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления (м/с)}\\$$
$$a_{x} - \text{ускорение с учетом направления (м/с²)} \\$$
$$t - \text{рассматриваемый промежуток времени (с) } \\$$
$$X - \text{конечная координата тела (м)} $$
4) Перемещение при равносукоренном движении (три формулы)
$$\boxed{ S_{x} = {V_{К_{x}}^2 - V_{0_{x}}^2 \over 2a_{x}} \text { [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{К_{x}} - \text{конечная скорость тела с учетом направления (м/с)} \\ $$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления(м/с)}\\ $$
$$a_{x} - \text{ускорение с учетом направления (м/с²)} \\ $$
$$ \boxed{S_{x} = {V_{К_{x}} + V_{0_{x}} \over 2} \cdot t \text{ [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления(м/с)} $$
$$V_{К_{x}} \text{ - конечная скорость тела с учетом направления (м/с) } $$
$$t - \text{Время} (с) $$
$$\boxed{ S_{x} = V_{0_{x}}\cdot t + {{a_{x} \cdot t^2 \over 2}} \text { [м]}}$$
$$S_{x} - \text{перемещение(м)} $$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления (м/с)}\\$$
$$a_{x} - \text{ускорение с учетом направления (м/с²)} \\$$
$$t - \text{рассматриваемый промежуток времени (с) } \\$$
5) Зависимость скорости от времени при равноускоренном движении
$$\boxed{ V_x(t) = V_{0_{x}} + {{a_{x} \cdot t}} \text { [м/c]}}\\$$
$$V_{0_{x}} - \text{начальная скорость тела с учетом направления(м/с)}$$
$$a_{x} - \text{ускорение с учетом направления (м/с²)} $$
$$t \text{ - рассматриваемый промежуток времени (с) } $$
$$V_{x} \text{ - конечная скорость тела с учетом направления (м/с)} $$
Динамика
6) Сила тяжести
$$ \boxed{\vec{F} = {m} \cdot {\vec{g}} \text{ [H]}}$$
$$ \vec{F} - \text{сила тяжести (H)} $$
$$ m - \text{ масса тела (кг)} $$
$$ {\vec{g}} - \text{ускорение свободного падения (м/с²)} $$
7) Сила упругости
$$ \boxed{{\vec{F}_{упр}} = {-k} \cdot {\Delta\vec{l}} \text{ [H]}}$$
$$ {\vec{F}_{упр}} - \text{сила упругости (H)} $$
$$ {k} - \text{коэффициент жесткости тела (H/м)} $$
$$ {\Delta\vec{l}} - \text{удлинение пружины (м)} $$
8) Сила трения скольжения
$$ \boxed{{{F}_{тр}} = {μ} \cdot {N} \text{ [H]}}$$
$$ {{F}_{тр}} - \text{сила трения (H)} $$
$$ {μ} - \text{коэффициент трения} $$
$$ N - \text{сила реакции опоры (H)} $$
9) Сила всемирного гравитационного притяжения
$$ \boxed{{F} = {{G} } \cdot{m_{1} \cdot m_{2} \over r^2 } \text{ [H]}}$$
$$ {F} - \text{сила гравитационного вазимодействия (H)} $$
$$ {G} - \text{гравитационная постоянная (H · м² / кг² )} $$
$$ m_{1} , m_{2} - \text{масса взаимодействующих тел (кг)} $$
$$ r - \text{ расстояние между телами (м)} $$
10) Сила Архимеда
$$ \boxed{{\vec{F}_{арх}} = {-ρ} \cdot {\vec{g}} \cdot {V_{погруж}}\text{ [H]}}$$
$$ {\vec{F}_{арх}} - \text{сила Архимеда (H)} $$
$$ {ρ} - \text{плотность жидкости или газа (кг/м³)} $$
$$ {\vec{g}} - \text{ускорение свободного падения (м/с²)} $$
$$ V_{погруж} - \text{ объем погруженной части тела (м³)} $$
11) Второй закон Ньютона
$$ \boxed{\vec{a} = \frac {\vec F} m\text{ [м/с²]}}$$
$$ \vec{a} - \text{ускорение тела с учетом направления (м/с²)} $$
$$ \vec {F} - \text{сумма всех сил действующих на тело, с учетом направления (H)} $$
$$m - \text{масса тела (кг)} $$
12) Третий закон Ньютона
$$ \boxed{\vec{F_{1_{2}}} = \vec{ -{F_{2_{1}}}}}$$
$$ \vec{F_{1_{2}}} - \text{сила, действующая на первое тело со стороны второго тела с учетом направления (H)} $$
$$ \vec{ -F_{2_{1}}} - \text{сила, действующая на второе тело со стороны первого с учетом направления (H)} $$
Третий закон Ньютона - при взаимодействии двух тел возникает пара сил, которые
1. равны по модулю
2. направлены вдоль одной прямой
3. противоположены по направлению
4. приложены к разным телам
5. силы одной природы
Статика
13) Момент силы
$$ \boxed{M = {F \cdot L} \text{ [Н · м]}} $$
$$M - \text{момент силы (Н · м)}$$
$$F - \text{сила (Н)} $$
$$L - \text{плечо силы (м)} $$
14) Коэффициент полезного действия
$$ \boxed{η = {{A_{полез} \over A_{затр}}} \ \cdot 100\% } $$
$$η - \text{К.П.Д. (%)}$$
$$A_{полез} - \text{работа, производимая механизмом над перемещаемым телом (Дж)}$$
$$A_{затр} - \text{работа, производимая над механизмом для приведения его в движение (Дж)}$$
15) Давление
$$ \boxed{P = {F_{⟂} \over S} \text{ [Па]}} $$
$$ P - \text{давление (Па)}$$
$$F_{⟂} - \text{сила, действующая перпендикулярно к поверхности (Н)} $$
$$S - \text{площадь поверхности (м²)} $$
16) Давление столба жидкости
$$ \boxed{P = {ρ \cdot g \cdot h} \text{ [Па]}} $$
$$ P - \text{давление (Па)}$$
$$ρ - \text{плотность жидкости (кг/м³)} $$
$$g - \text{ускорение свободного падения (м/с²)} $$
$$h - \text{расстояние от исследуемой точки до свободной поверхности жидкости (м)} $$
Законы Сохранения
17) Механическая работа
$$\boxed{ {A} = {F \cdot \Delta X \cdot cos\ 𝜑 } \text{ [Дж]}}$$
$$A - \text{Механическая работа (Дж)}$$
$$F - \text{постоянная сила, действующая на тело (Н)}$$
$$\Delta X - \text{изменение координат тела (м)}$$
$$cos\ 𝜑 - \text{косинус угла между направлением силы и перемещением}$$
18) Мощность
$$\boxed{ {N} = {A \over t } \text{ [Вт]}}$$
$$N - \text{мощность (Вт)}$$
$$A - \text{работа (Дж)}$$
$$t - \text{время (с)}$$
19) Кинетическая энергия
$$\boxed{ {K} = {{m}\ \cdot v^2 \over 2 } \text{ [Дж]}}$$
$$K - \text{кинетическая энергия (Дж)}$$
$$m - \text{масса тела (кг)}$$
$$v - \text{скорость тела (м/с)}$$
20) Потенциальная энергия тела вблизи поверхности Земли
$$\boxed{ {П} = {{m}\ \cdot g \cdot h } \text{ [Дж]}}$$
$$П - \text{потенциальная энергия (Дж)}$$
$$m - \text{масса тела (кг)}$$
$$g - \text{ускорение свободного падения (м/с²)}$$
$$h - \text{высота над поверхностью Земли (м)}$$
21) Потенциальная энергия сжатой пружины
$$\boxed{ {П} = {{k}\ \cdot \Delta x^2 \over 2 } \text{ [Дж]}}$$
$$П - \text{потенциальная энергия (Дж)}$$
$$k - \text{коэффициент жесткости пружины (Н/м)}$$
$$\Delta x - \text{величина на которую сжата или растянута пружина (м)}$$
22) Закон сохранения энергии (формула + формулировка)
$$ \boxed{E_{к1} + E_{п1} = E_{к2} + E_{п2}} $$
$$E_{к1} - \text{начальная кинетическая энергия (Дж)}$$
$$E_{п1} - \text{начальная потециальная энергия (Дж)}$$
$$E_{к2} - \text{конечная кинетическая энергрия (Дж)}$$
$$E_{п2} - \text{конечная потенциальная энергия (Дж)}$$
$$Закон \ сохранения \ энергии \text{ - суммарная энергия системы не меняется в процессе взаимодействия, если система замкнута и нет сил трения.} $$
23) Связь между работой и энергией
$$\boxed{ {Е} = {Е_{o} + А_{тр}+А_{внешн}} \text{ [Дж]}}$$
$$Е - \text{механическая энергия (Дж)}$$
$$Е_{o} - \text{начальная механическая энергия (Дж)}$$
$$А_{тр} - \text{работа внутренних сил трения (Дж)}$$
$$А_{внешн} - \text{внешняя работа (Дж)}$$
Термодинамика
24) Внутренняя энергия (определение)
$$Внутренняя \ энергии \text{ - сумма кинетических энергий хаотического движения молекул относительно центра масс и потенциальных энергий взаимодействия молекул друг с другом, но не с молекулами другого тела} $$
25) Относительная влажность воздуха
$$ \boxed{𝜑 = {P_{t} \over P_{н.п. t}} \ \cdot 100\% } $$
$$𝜑 - \text{относительная влажность воздуха}$$
$$P_{t} - \text{давление пара в данный момент времени, при данной температуре (Па)}$$
$$P_{н.п. t} - \text{давление насыщенного пара при данной температуре (Па)}$$
26) Насыщенный пар (определение)
$$Насыщенный \ пар \text{ - это пар находящийся в динамическом равновессии со своей жидкостью} $$
27) Теплоёмкость вещества
$$ \boxed{C = {Q \over \Delta T} \text{ [Дж/К]}}$$
$$C - \text{Теплоёмкость вещества (Дж/К)}$$
$$Q - \text{количество теплоты (Дж)}$$
$$\Delta T - \text{температура (К)}$$
28) Удельная теплоёмкость вещества
$$ \boxed{c = {Q \over m \cdot \Delta T} \ \Big[{\text{Дж} \over {{\text{кг} \cdot \text{К}}}}\Big] } $$
$$c - \text{удельная теплоемкость тела} \ \Big({\text{Дж} \over {{\text{кг} \cdot \text{К}}}}\Big)$$
$$Q - \text{количество теплоты (Дж)} $$
$$m - \text{масса (кг)}$$
$$\Delta T - \text{изменение температуры (К)} $$
29) Удельная теплота сгорания топлива
$$Удельная \ теплота \ сгорания \ топлива \text{ - показывает какое кол-во теплоты выделяется при полном сгорании одного килограмма топлива } $$
$$ \boxed{Q = q \cdot m \text{ [Дж]}} $$
$$Q - \text{количество теплоты (Дж)}$$
$$q - \text{удельная теплота сгорания топлива (Дж/кг)}$$
$$m - \text{масса (кг)}$$
30) Удельная теплота плавления
$$ \boxed{Q = λ \cdot m \text{ [Дж]}} $$
$$Q - \text{количество теплоты (Дж)} $$
$$λ - \text{удельная теплота плавления (Дж/кг)} $$
$$m - \text{масса (кг)}$$
31) Удельная теплота парообразования
$$ \boxed{Q = L \cdot m \text{ [Дж]}} $$
$$Q - \text{количество теплоты (Дж)}$$
$$L - \text{удельная теплота парообразования (Дж/кг)}$$
$$m - \text{масса (кг)}$$
32) Уравнение теплового баланса
$$ \boxed{Q_{отд} = Q_{пол} } $$
$$Q_{отд} - \text{отданное количество теплоты (Дж)} $$
$$Q_{пол} - \text{полученное количество теплоты (Дж)} $$
33) Уравнение Клапейрона-Менделеева
$$ \boxed{P \cdot V = \vartheta \cdot R \cdot T} $$
$$ P - \text{давление (Па)}$$
$$ V - \text{объем (м³)} $$
$$\vartheta - \text{количество вещества (моль)} $$
$$R - \text{универсальная газовая постоянная} \ \Big({\text{Дж} \over {{\text{К} \cdot \text{моль}}}}\Big) $$
$$T - \text{температура (К)} $$
34) Закон Дальтона (определение)
$$Закон \ Дальтона \text{ - давление смеси газов равно сумме парциальных давлений каждого газа в составе смеси} $$
35) Первый закон термодинамики (формула)
$$ \boxed{\Delta U + А = Q} $$
$$U - \text{изменение внутренней энергии (Дж)}$$
$$А - \text{работа совершенная системой (Дж)} $$
$$Q - \text{количество теплоты , переданное системе (Дж)} $$
36) Первое начало термодинамики (для каждого изопроцесса)
1) Изохорный
$$ \boxed{Q = \Delta U} $$
$$Q - \text{теплота (Дж)} $$
$$\Delta U - \text{изменение внутренней энергии (Дж)}$$
2) Изобраный
$$ \boxed{Q = \Delta U + P \ \cdot \ (V_{2} - V_{1}) \text{ [Дж]}} $$
$$Q - \text{теплота (Дж)} $$
$$\Delta U - \text{изменение внутренней энергии (Дж)}$$
$$P - \text{давление (Па)} $$
$$V_{2} - \text{конечный объем (м³)}$$
$$V_{1} - \text{начальный объем (м³)}$$
3) Изотермический
$$ \boxed{Q = A} $$
$$Q - \text{теплота (Дж)} $$
$$А - \text{работа (Дж)} $$
37) Адиабатический процесс (определение+формула)
$$Адиабатный \ процесс \text{ - это процесс проходящий без теплообмена с окружающей средой} $$
$$ \boxed{А = - \Delta U} $$
$$А - \text{работа (Дж)} $$
$$\Delta U - \text{изменение внутренней энергии (Дж)}$$
38) Работа идеального газа (формула)
$$ \boxed{A = P \cdot \Delta V \text{ [Дж]} } $$
$$A - \text{работа (Дж)} $$
$$P - \text{давление (Па)}$$
$$\Delta V - \text{изменение объема (м³)} $$
39) Коэффициент полезного действия теплового двигателя (формула)
$$ \boxed{η = {\Big(1 - {Q_{х} \over Q_{н}}\Big)} \ \cdot 100\% } $$
$$η - \text{К.П.Д. тепловой машины}$$
$$Q_{х} - \text{теплота холодильника (Дж)}$$
$$Q_{н} - \text{теплота нагревателя (Дж)}$$
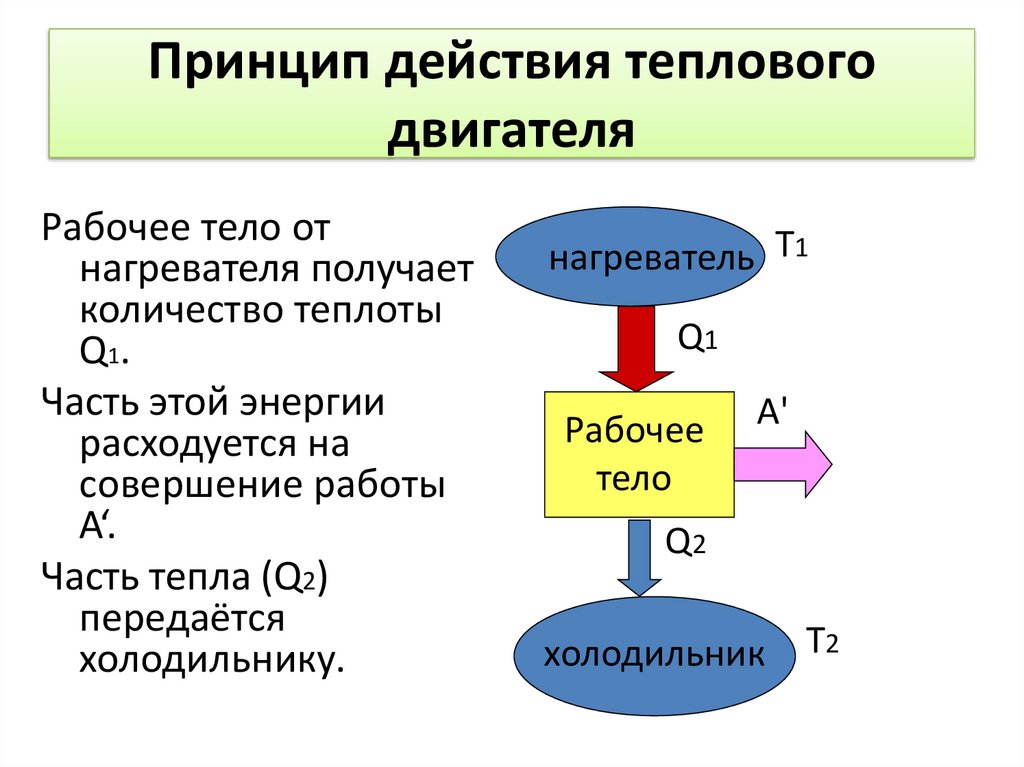
40) Принципиальная схема действия любого теплового двигателя